Pruebas Estadísticas II

Prueba de la distancia: Esta prueba puede ser realizada de dos maneras: considerando a los números pseudoaleatorios generados como dígitos, o considerando como números reales.

1. Números pseudoaleatorios considerados como dígitos. Si los números pseudoaleatorios generados son considerados como dígitos, entonces la prueba consiste en contar el número de dígitos que aparece entre ocurrencias sucesivas de un mismo dígito. El estadístico que se utiliza para esta prueba se obtiene como:

El cual se compara con X²_{α, n}. Si X²₀ <  X²_{α, n}. entonces los números pseudoaleatorios pasan la prueba de la distancia. Es muy importante señalar que el valor seleccionado de n, debe ser tal que la suma de las frecuencias esperadas de todos los tamaños sea mayor que 5. A continuación se muestra la tabla de frecuencias esperadas de todos los tamaños de hueco, considerando a los números pseudoaleatorios generados como dígitos:

       Fuente: COSS BU, Raúl. Simulación un enfoque práctico. Pág 36.



2. Números pseudoaleatorios considerados como números reales. Si los números pseudoaleatorios generados son considerados como números reales, entonces, para realizar esta prueba es necesario seleccionar un intervalo (α ; β), el cual debe de estar contenido en el intervalo (0 ; 1), es decir, 0≤α≤β≤1. En seguida, para cada número pseudoaleatorio generado se pregunta si es o no elemento del intervalo (α ; β). Si U_J (Número uniforme generado) es el elemento de (α ; β), U_J+I+1 vuelve a ser elemento de (α ; β) entonces se tiene un hueco de tamaño i. Por ejemplo, si α=0.3 y β=0.5 y los números pseudoaleatorios generados son como sigue: 0.32415, 0.22257, 0.19147, 0.75103, 0.49383, entonces el hueco es de tamaño 3.

Para el caso de considerar los números pseudoaleatorios generados como números reales, la distribución de probabilidad del tamaño del hueco es como sigue:

P_I = θ(1-θ)^I Para i = 0,1,2…
Donde θ= β-α representa la probabilidad de caer en el intervalo (α ; β).

Al igual que en el inciso anterior, es conveniente agrupar las probabilidades para valores de i ≥ n. Tal agrupación se obtiene con la siguiente expresión:

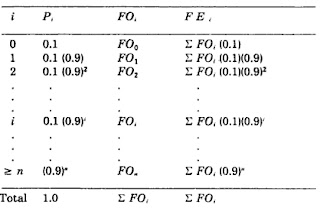
Con estas ecuaciones se obtienen las frecuencias esperadas y observadas para los diferentes tamaños de hueco, considerando a los números pseudoaleatorios generados como números reales tal y como se muestra:

Utilizando la ecuación de X²₀ y comparando el resultado con la ecuación de X²_{α, n} se toma la decisión de aceptar o rechazar la prueba de la distancia. Es muy importante señalar que el valor de α y β no tiene ninguna influencia en la bondad de la prueba, y también es necesario señalar que el valor de n debe ser seleccionado de acuerdo al criterio mencionado.

Prueba de chi-cuadrado: Esta prueba se usa cuando se quiere probar la hipótesis de que unos datos muéstrales provienen de una determinada distribución.

La prueba chi cuadrado se basa en la comparación entre la frecuencia observada en un intervalo de clase y la frecuencia esperada en dicho intervalo, calculada de acuerdo con la hipótesis nula formulada. Es decir, se quiere determinar si las frecuencias observadas en la muestra están lo suficientemente cerca de las frecuencias esperadas bajo la hipótesis nula.

Para esta prueba es necesario agrupar o distribuir las observaciones de la muestra en intervalos de clase, preferiblemente del mismo tamaño. El estadístico de prueba está definido como:

Donde: Oi = Total de valores que caen en el intervalo i.

Ei = Número esperado de valores en el intervalo i.

k = Número de intervalos de clase en que se distribuyen las observaciones.

Si los límites del intervalo de clase i están dados por Xi-1 y Xi, como lo ilustra la presente gráfica, el número esperado de observaciones para ese intervalo está dado por:

Ei =nPi

Donde Pi representa la probabilidad de que una observación quede en el intervalo i, de acuerdo con función de densidad que se esté analizando, y n es el número total de observaciones.

La probabilidad de que una observación caiga en el intervalo i está dada por:

Donde f0(x, θ) es la función de densidad de la variable aleatoria X, bajo la hipótesis nula.

Para ver que distribución sigue el estadístico X², considere la siguiente situación:

Suponga que las observaciones de la muestra pueden clasificarse en dos intervalos o categorías. Sea Y1 el número de observaciones que caen en la categoría 1, y sea P1 su respectiva probabilidad.

Si el tamaño de muestra es lo suficientemente grande, Y1 (que sigue una distribución binomial) puede aproximarse por una distribución normal con valor esperado nP1 y varianza nP1 (1-P1). Por lo tanto, la variable Z definida a continuación sigue una distribución normal estándar, y Z² una distribución chi cuadrado con un grado de libertad.

Si definimos Y2 como Y2 = n - Y1, y P2 = 1 - P1, se tiene que Z² se puede desarrollar  de la siguiente manera:

Ahora suponga que las observaciones pueden clasificarse no en dos sino en k clasificaciones mutuamente excluyentes, y sean Yi y Pi el número de variables que caen en la categoría i y la probabilidad respectiva. La distribución conjunta de Y1, Y2,...,Yk tiene una distribución multinomial con parámetros n, P1, P2,... y Pn, donde Pk = 1 - P1 - P2 -... -Pk-1. Se puede demostrar que la variable Z2 definida a continuación sigue una distribución chi cuadrado con k-1 grados de libertad:

Comparando la expresión anterior con el estadístico X² definido previamente, vemos que este estadístico sigue también la distribución chi cuadrado con k - 1 - p grados de libertad, siendo p el número de parámetros estimados para definir completamente la función f0(x,θ). Sin embargo para que esta suposición sea válida se requiere que el número esperado de observaciones en cada intervalo de clase sea por lo menos 5. Si esta condición no se cumple, es necesario agrupar en uno los resultados de varios intervalos de clase.

Algunas consideraciones que hay que tener en cuenta con respecto a la aplicación de esta prueba son las siguientes:

1. El número de intervalos de clase debe ser por lo menos cinco. Para facilidad de los cálculos y la identificación de la posible distribución tampoco debería ser muy grande.

2. El número esperado de observaciones en cada intervalo debe ser mayor o igual a cinco; en caso contrario, deberían agruparse varios intervalos para lograr esto.

3. Al realizar los cálculos para Pi hay que tener en cuenta los intervalos extremos como casos especiales, a saber:

Cálculo de P1. Aunque el primer intervalo incluye aquellos valores observados que están ente X0 y X1, sólo corresponde a los resultados de una muestra. El hecho de que no se hayan observado en la muestra valores menores o iguales que x0 no implica que en la población de donde se toma la muestra no se puedan presentar valores menores o iguales que x0. Por lo tanto, el cálculo de P1 corresponde a la probabilidad de que la variable aleatoria sea menor o igual que X1, y no únicamente entre X0 y X1.

Es decir,

Cálculo de Pn. De manera similar, el último intervalo corresponde no sólo a los valores que están entre Xk-1 y Xk, sino que comprende también los valores de la población que sean mayores que Xk, así éstos no se hayan presentado en la muestra. Por lo tanto, Pk se calcula como:

Fuente: SERRANO CAMPOS, Eduardo. Simulación de sistemas. 26 de septiembre de 2009.